Based on the given information, the area of the shaded region is approximately 19.6
 . Option 3
. Option 3
How to calculate area of shaded region
Given:
Radius of the circle = 6 cm
To find the shaded area (outside the regular hexagon but inside the circle), find the area of the circle and subtract the area of the regular hexagon.
Area of the Circle:
The formula for the area of a circle is
π
 .
.
So, the area of the circle with a radius of 6 cm is
π ×
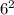
=36π
 .
.
Area of the Regular Hexagon:
The hexagon is inscribed in the circle, and its side length is equal to the radius of the circle.
The formula for the area of a regular hexagon is
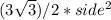
For the side length of 6 cm, the area of the regular hexagon is
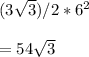
 .
.
Now, to find the shaded area, subtract the area of the hexagon from the area of the circle:
Shaded area = Area of circle - Area of hexagon
Shaded area = 36π−54
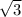
Approximating the values:
Shaded area ≈ 113.1−93.53=19.57

Rounded to one decimal place, the area of the shaded region is approximately 19.6
 .
.