Question

1. A 1.32 x 104 meter steel railroad track with a coefficient of linear expansion of 12 x 10-6 per degree Celsius changes temperature from 12°C to 37°C. By how many meters will the railroad tracks expand?

2. Railroad tracks are segmented into short pieces. Why is this a good idea?
3. The Eiffel Tower in Paris is 352 meters tall, and is made primarily of iron, which has a coefficient of linear expansion of 12 x 10-6. The average low in Paris is 3°C and the average high is 27°C. What is average change in height the tower experiences each year?
4. By how much would you need to heat a 13.0 foot bar of zinc to make it expand by one inch? The coefficient of linear expansion of zinc is 30 x 10-6 per degree Celsius.
5. A metal bar changes in length by 1.00 meter with a 150 degree Celsius change in temperature. It’s coefficient of linear expansion is 25 x 10-6 per degree Celsius. What is the metal bar’s original length?

6. An unknown metal alloy is being tested to discover its thermal properties to see if it is suitable for use as a component in an aircraft wing. The alloy is formed into a bar measuring 3.00 meter in length and is then heated from its starting temperature of 30 degrees Celsius to a final temperature of 110 degrees Celsius. The length of the heated bar is measured to be exactly 1.002 meters in length. What is the coefficient of thermal expansion of the alloy to 2 significant figures?
7. The aircraft wing from problem 6 experiences temperature extremes that span 210 degrees Celsius. The component for the wing will have a length of 3.00 meters. Testing indicates that the aircraft wing will remain stable only if the component never expands to a length larger than 3.017 meters. If the component is made from the metal alloy in question, will it meet this requirement?
8. A rod 3.2 m long expands 0.50 mm when heated from 20°C to 84°C. What is the coefficient of linear expansion of the material from which the rod is made?
9. A steel girder is 32.10 m at 22°C. If the temperature drops to 8.0°C, what is the length of the girder? Answer to 2 decimal places.
10. A metal rod has a length of 123. cm at 200°C. At what temperature will the length be 92.6 cm if the coefficient of linear expansion of the material in the rod is 2.0 x 10-5 °C-1?

Answer 1

1) 0.1584 m

2) To allow for expansion without derailment

3) 0.101376 m

4) 213.675 °C

5) 266.67 m

6) 8.33 × 10⁻⁶ /°C

7) The alloy meets the requirement

8) 1.95 × 10⁻³ /°C

9) 32.095 m

10) -12157.72°C

Step-by-step explanation:

1) Equation for the coefficient of linear expansion =
`(\Delta L)/(L) = \alpha _L \Delta T`

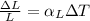
Where:

ΔL = Change in length = Required

L = Initial length = 1.32 × 10⁴ m

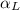`\alpha _L` = Coefficient of linear expansion of steel = 12 × 10⁻⁶ /°C

ΔT = Change in temperature = 37°C - 27°C = 10°C

Plugging the values in the equation for the temperature expansion of steel, we have m;

ΔL = L ×
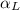`\alpha _L` ×ΔT = 1.32 × 10⁴ × 12 × 10⁻⁶ × 10 = 0.1584 m

2. Here we have that by segmenting railroad tracks into short pieces, the expansion of the metal tracks with temperature can be absorbed by the gaps between the segment without distorting the shape and direction (pattern) of the tracks

3. Here we have;

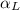`\alpha _L` = Coefficient of linear expansion of iron = 12 × 10⁻⁶ /°C

ΔT = Temperature change = 27°C - 3°C = 24°C

L = Height of the Eiffel Tower = 352 meters

∴ ΔL = L ×
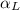`\alpha _L` ×ΔT = 352 × 12 × 10⁻⁶ × 24 = 0.101376 m

Therefore, the height of the Eiffel Tower changes from 352 m to about 352.101376 m each year, with an average change in height experienced each year = 0.101376 m

4. Here, we have

L = 13.0 ft

ΔL = 1 in.

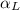`\alpha _L` = 30 × 10⁻⁶ /°C

ΔT = Required temperature change

From
`(\Delta L)/(L) = \alpha _L \Delta T`

`\Delta T =(\Delta L)/(L * \alpha _L) = (1)/(156 * 30 * 10^(-6)) = 213.675^(\circ)C`

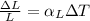
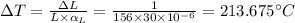
5. Here, we have;

`L = (\Delta L)/(\alpha _L \Delta T)`

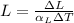
∴ L = 1/(150×25 × 10⁻⁶) = 266.67 m

The bars original length = 266.67 m

6. Here we have;

`\alpha _L = (\Delta L)/(L * \Delta T)`

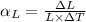
Where:

ΔL = 3.00 - 3.002 = 0.002 m

L = 3.00 m

ΔT = 110°C - 30°C = 80°C

∴
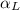`\alpha _L` = 0.002/(3.00 × 80) = 8.33 × 10⁻⁶ /°C

7. Here we have;

ΔL = L ×
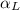`\alpha _L` ×ΔT = 3 × 8.33 × 10⁻⁶ × 210 = 0.00525 m

Therefore, final length = 3.00 m + 0.00525 m = 3.00525 m

Since 3.00525 m < 3.017 m hence the alloy meets the requirement.

8. Here, we have

L = 3.2 m

ΔL = 0.5 m

ΔT = 84°C - 24°C = 60°C

∴
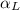`\alpha _L` = 0.5/(3.2 × 60) = 1.95 × 10⁻³ /°C

The coefficient of linear expansion of the material from which the rod is made = 1.95 × 10⁻³ /°C

9. Here, we have

Length of steel girder, L = 32.10 m

ΔT = 8°C - 22°C = -14°C

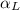`\alpha _L` = 12 × 10⁻⁶ /°C

ΔL = L ×
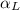`\alpha _L` ×ΔT

Hence ΔL = 32.1 × 12 × 10⁻⁶× -14 = -0.0054 m

New length = 32.1 - 0.0054 = 32.095 m

10. Here we have;

ΔL = 92.6 cm - 123 cm = -30.4 cm

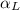`\alpha _L` = 2.0 × 10⁻⁵ /°C

L = 123 cm

∴
`\Delta T =(\Delta L)/(L * \alpha _L) = (-30.4)/(123 * 2.0 * 10^(-5)) = -12357.724^(\circ)C`

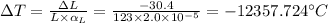
Therefore, the temperature will be 200 - 12357.724 = -12157.72°C.