Answer:
C. 50
Explanation:
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence level of
, and a confidence level of
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.

In which
z is the zscore that has a pvalue of
 .
.
The margin of error is:
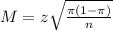
The higher the margin of error, the wider an interval is.
As the sample size increases, the margin of error decreases. If we want a widest possible interval, we should select the smallest possible confidence interval.
So the correct answer is:
C. 50