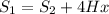Answer:
The bases are congruent.
The volume of the first solid is twice as much as the volume of the second solid.
If the dimensions of the second solid are x by x by h, the first solid has 4xh more surface area than the second solid.
Explanation:
From the above answers; the term congruent means two similar objects or shapes having the same pattern or structure. From the question; we are being told that the two rectangular solid have a square base hence; they are both congruent in nature .
Also;
The volume of the first solid is twice as much as the second solid . i.e 2:1
If the volume of the first solid is :
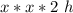 =
=
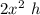
Then the volume of the second solid is =
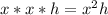
thus ; they are in the ratio of 2:1
FInally: If the dimensions of the second solid are x by x by h, the first solid has 4xh more surface area than the second
The surface area of the first solid is :
![=2[x*x+(2 H*x+2 H*x)] \\ \\ =2[x^2+4 Hx] \\ \\ = 2x[x + 4Hx]](https://img.qammunity.org/2021/formulas/mathematics/college/qimpcqt6yjrmtlwe87p57301stkcv9zt4t.png)
Then the second solid is :
![2[x*x+x* H+ H*x] \\ \\ =2[x^2+2 Hx] \\ \\ =2x[x+ 2H]](https://img.qammunity.org/2021/formulas/mathematics/college/qxksc5a1b2kuevhle7rb0ik8t17er1ifcl.png)
Therefore: