Answer:
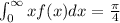
Explanation:
We need to find the integrate of:
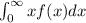
Let's use the integration by parts rule.
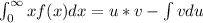 (1)
(1)
 and
and
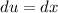
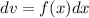 and
and
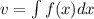
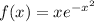
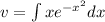 if we use change variable we can solve it, we can do
if we use change variable we can solve it, we can do
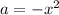 then
then

So we have:
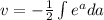
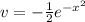
Using this in (1) we have:
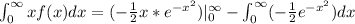
The used criteria to make the first term zero is because the exponential tends to zero faster than the x tends to infinity.
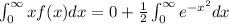
We know that the integral from 0 to infinity of
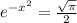 , hence:
, hence:
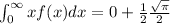
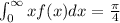
I hope it helps you!