Question

Compare the volume and surface area of a sphere with a radius of 7 cm with that of a cube that has sides measuring 11.27 cm.

1. The volume of the sphere is approximately equal to the volume of the cube, but the sphere has a greater surface area.


2. The volume of the sphere is approximately equal to the volume of the cube, but the cube has a greater surface area.


3. The volume of the cube is greater than the volume of the sphere, but the sphere has a greater surface area.


4. The sphere and the cube have approximately the same volume and surface area.

Answer 1

2. The volume of the sphere is approximately equal to the volume of the cube, but the cube has a greater surface area.

Explanation:

Sphere

Radius =7cm

`\text{Volume of a Sphere}=(4)/(3)\pi r^3\\=(4)/(3)\pi *7^3\\=1436.76\approx 1400cm^3`

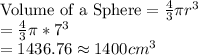
Surface Area of a Sphere
`=4\pi r^2`

`=4\pi *7^2 = 615.75cm^2`

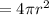
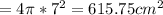
Cube

Side Length=11.27cm

`\text{Surface Area=}6l^2=6*11.27^2=762.08cm^2\\\text{Volume = }l^3=11.27^3=1431.44\approx 1400cm^3`

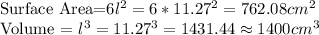
Therefore:

The volume of the sphere is approximately equal to the volume of the cube, but the cube has a greater surface area.