Answer:
The volume of metal used is 141π cubic inches.
The total surface area to be powder-coated is 1,266.13π square inches.
Explanation:
The pipe is formed by two cylinder.
We know that the height of the pipe is 4 feet, which is equivalent to 48 inches, because 1 feet equals 12 inches. So, the height of both cylinders is 48 inches.
Now, the volume of a circular cylinder is

Where
 is the radius and
is the radius and
 is the height.
is the height.
For the outside cylinder, we have

For the inner cylinder, we have

Notice that the volume of the pipe is difference between the outside cylinder and the inside cylinder

Therefore, the volume of metal used is 141π cubic inches.
Now, the total surface is sum of the surface of both cylinders.
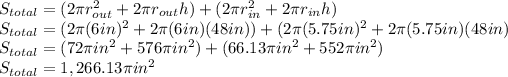
Therefore, the total surface area to be powder-coated is 1,266.13π square inches.