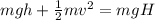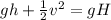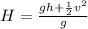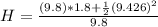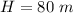Question

"A small lead ball, attached to a 1.50-m rope, is being whirled in a circle that lies in the vertical plane. The ball is whirled at a constant rate of three revolutions per second and is released on the upward part of the circular motion when it is 1.8 m above the ground. The ball travels straight upward. In the absence of air resistance, to what maximum height above the ground does the ball rise?

Answer 1

The maximum height is
`H =80 \ m`

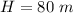
Step-by-step explanation:

From the question we are told that

The length of the rope is
`r = 1.50 \ m`

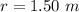
The rate at which the ball was whirled is
`R = 3 rps`

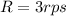
The height above the ground when released is
`h = 1.8 \ m`

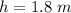
The initial velocity of the ball is mathematically represented as

`v = (d)/(t)`

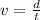
Where d is the distance which is the circumference of the circular which can be calculated as

`d = 2 \pi r`

`d = 2 * 3.143 * 1.5`

`d =9.426 \ m`

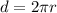
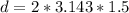
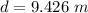
Now the time is 1 second as stated in the question so

`v =(9.426)/(1)`

`v =9.426 \m/s`

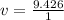
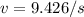
From the law of energy conservation

`PE + KE = PE_(max)`

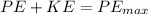
Where PE is the potential energy at the first height stated in the question

Which is mathematically represented as

`PE = mgh`

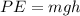
KE is the kinetic energy at the first level which is mathematically represented as

`KE = (1)/(2) m v^2`

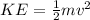
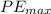`PE_(max)` is the potential energy at the maximum height which is mathematically represented as

`PE_(max) = mgH`

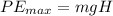
Where H is the maximum height

So

`mgh + (1)/(2) mv^2 = mgH`

`gh + (1)/(2) v^2 = gH`

`H = (gh + (1)/(2) v^2 )/(g)`

`H = ((9.8 ) * 1.8 + (1)/(2) (9.426)^2 )/(9.8)`

`H =80 \ m`

Answer 2

42.7m

Step-by-step explanation:

Given:

h'= 1.8 m

r= 1.5 m

ω = 3 rev/s

ω = 3 ₓ 2 π rad/s =>6 π rad/s

Speed of the ball 'V' when it releases from the rope is given by,

V= ω x r

V= 6 π x 1.5

V=28.3 m/s

As we know that acceleration due to gravity always in downward direction.

`V_f^2=V_o^2+2as`

The final speed will be zero

`0=28.3^2 - 2(9.8)(h)`

h = 40.8 m

So the height from the ground,H = h' + h

H= 40.8 + 1.8 =42.7m