Answer:
The required recursive formula is
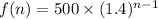
Explanation:
Mohamed decided to track the number of leaves on the tree in his backyard each year.
The first year there were 500 leaves
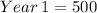
Each year thereafter the number of leaves was 40% more than the year before so that means

For the third year the number of leaves increase 40% than the year before so that means

Similarly for fourth year,
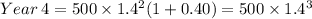
So we can clearly see the pattern here
Let f(n) be the number of leaves on the tree in Mohameds back yard in the nth year since he started tracking it then general recursive formula is
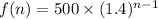
This is the required recursive formula to find the number of leaves for the nth year.
Bonus:
Lets find out the number of leaves in the 10th year,
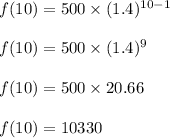
So there will be 10330 leaves in the 10th year.