Answer:
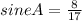
Explanation:
The tangent ratio:
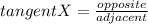
It really helps to draw a model. The given angle will not be the 90° (this is never used), and it doesn't matter in which angle you choose to put it. Label that angel A. Now, from the angel, go to the side opposite the angel and label that side as 8. Then do the same for the adjacent and label it 15.
For the sine ratio:
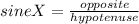
You need the hypotenuse. You can find this by using the Pythagorean theorem:

a and b are the legs (given) and c the hypotenuse. Insert the values:
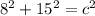
Solve for c. Simplify exponents:
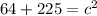
Add:

Find the square root of both sides:
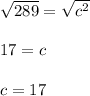
The hypotenuse is 17. You can now insert the values for sine:

Done :D