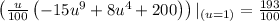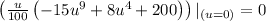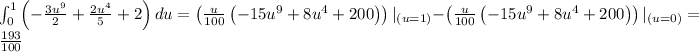Question

Please help with this Calculus questions

Answer 1

`\int_(0)^(1)\left( - (3 u^(9))/(2) + (2 u^(4))/(5) + 2 \right)du=(193)/(100)=1.93`.

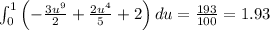Explanation:

To find
`\int_(0)^(1)\left( - (3 u^(9))/(2) + (2 u^(4))/(5) + 2 \right)du`.

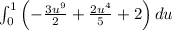First, calculate the corresponding indefinite integral:

Integrate term by term:

`\int{\left(- (3 u^(9))/(2) + (2 u^(4))/(5) + 2\right)d u}} =\int{2 d u} + \int{(2 u^(4))/(5) d u} - \int{(3 u^(9))/(2) d u}`

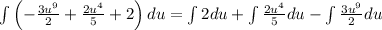
Apply the constant rule
`\int c\, du = c u`

`\int{2 d u}} + \int{(2 u^(4))/(5) d u} - \int{(3 u^(9))/(2) d u} = {\left(2 u\right)} + \int{(2 u^(4))/(5) d u} - \int{(3 u^(9))/(2) d u}`

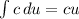
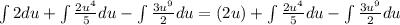
Apply the constant multiple rule
`\int c f{\left(u \right)}\, du = c \int f{\left(u \right)}\, du`

`2 u - {\int{(3 u^(9))/(2) d u}} + \int{(2 u^(4))/(5) d u} = 2 u - {\left((3)/(2) \int{u^(9) d u}\right)} + \left((2)/(5) \int{u^(4) d u}\right)`

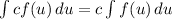
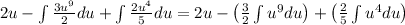
Apply the power rule
`\int u^(n)\, du = (u^(n + 1))/(n + 1)`

`2 u - (3)/(2) {\int{u^(9) d u}} + (2)/(5) {\int{u^(4) d u}}=2 u - (3)/(2) {(u^(1 + 9))/(1 + 9)}+ (2)/(5){(u^(1 + 4))/(1 + 4)}`

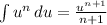
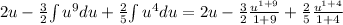
Therefore,

`\int{\left(- (3 u^(9))/(2) + (2 u^(4))/(5) + 2\right)d u} = - (3 u^(10))/(20) + (2 u^(5))/(25) + 2 u = (u)/(100) \left(- 15 u^(9) + 8 u^(4) + 200\right)`

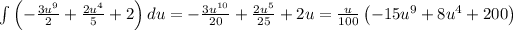
According to the Fundamental Theorem of Calculus,
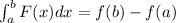`\int_a^b F(x) dx=f(b)-f(a)`, so just evaluate the integral at the endpoints, and that's the answer.

`\left((u)/(100) \left(- 15 u^(9) + 8 u^(4) + 200\right)\right)|_(\left(u=1\right))=(193)/(100)`

`\left((u)/(100) \left(- 15 u^(9) + 8 u^(4) + 200\right)\right)|_(\left(u=0\right))=0`

`\int_(0)^(1)\left( - (3 u^(9))/(2) + (2 u^(4))/(5) + 2 \right)du=\left((u)/(100) \left(- 15 u^(9) + 8 u^(4) + 200\right)\right)|_(\left(u=1\right))-\left((u)/(100) \left(- 15 u^(9) + 8 u^(4) + 200\right)\right)|_(\left(u=0\right))=(193)/(100)`