Answer:

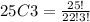
And using properties for the factorial term we can do this:
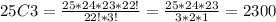
So then we will have 2300 possible sequences of plays with the conditions required
Explanation:
For this case we can use the formula for cominatory since for this case theorder in which we select the 3 plays from the total of 25 is no matters. We can use the term (nCx) who means combinatory and it's given by this formula:
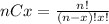
And for this casr the different sequences of plays do they have are given by 25C3, replacing into the formula we got:

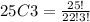
And using properties for the factorial term we can do this:
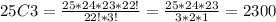
So then we will have 2300 possible sequences of plays with the conditions required