Correct question :
The average speed that a tsunami (a large tidal wave) travels is represented
by the function
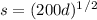 where s is the speed (in miles per hour) that the tsunami is traveling and d is the average depth (in feet) of the wave.
where s is the speed (in miles per hour) that the tsunami is traveling and d is the average depth (in feet) of the wave.
a. Find the inverse of the function.
b. Find the average depth of the tsunami when the recorded speed of the wave is 250 miles per hour.
Answer:
a)
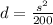
b) 312.5 ft
Explanation:
Given:
Average speeds,
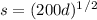
a) To find the inverse of the function.
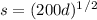
s² = 200d
200d = s²
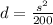
Therefore, inverse of the function =
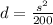
b) average depth when speed is 250 miles per hour.
Average depth = d
Therefore, let's use the formula :
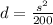
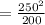
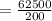
d = 312.5 feet
The average depth when speed is 250 miles per hour is 312.5 ft