Question

One positive integer is 7 less than twice another. The sum of their squares is 346. Find the integers. should be 2 answers

Answer 1

the two positive integers are x= 15, and y = 11

Explanation:

Let the first integer be x

Let the second integer be y

from the problem we can decode the following equations

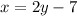`x=2y-7` ---------------------------- equation 1

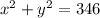`x^(2) + y^(2)= 346` -------------------------equation 2

substituting the value of x into equation 2, we have

`(2y-7)^(2) + y^(2)= 346 --------------equation 3`

expanding, we have

`4y^(2)-28y+49+y^(2)=346`

`5y^(2)-28y-297 = 0`

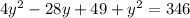
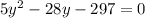
from this, y = 11 or y = -5.4

since our answer is a positive integer, we will have to pick the first value of y which is y = 11

substituting the value of y into equation 1, we have

`x= 2(11)-7=15`

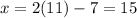
hence x = 15

Therefore, we have x= 15, and y = 11

these are the two positive integers