Hey there!
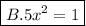
Let's solve each equation one by one to figure out which one is correct.
A.
x^2 = -100
Square root both sides.
x = √-100
A square root of a negative number is not a real number, so this option is incorrect.
B.
5x^2 = 1
Divide each side by 5.
x^2 = 1/5
Find the square root of each side.
x = ±0.447
The two solutions are positive 0.447 and -0.447 because those both equal 1/5 when squared. So this is the equation that has two real solutions. But let's keep solving to show why the other answers are wrong.
C.
6x^2 + 17 = 11
Subtract 17 from each side.
6x^2 = -6
Divide each side by 6
x^2 = -1
Square root each side.
x = √-1
A square root of a negative number is not a real number, so this option is incorrect.
D.
7(x^2 + 6) = 42
Divide each side by 7.
x^2 + 6 = 6
Subtract 6 from each side.
x^2 = 0
Square root of each side.
x = √0 = 0
The square root of 0 is just 0, there is only one solution.
So, the answer is B.
Hope this helps!