Question

The salary of employees at a company follows normal distribution. The mean salary of the employees is $5000 with a standard deviation of $500. In a simple random sample of 40 employees, what is the probability that the salary of a randomly selected employee will be less than $4900?

Answer 1

answer is 50%

Explanation:

Answer 2

Given Information:

Mean salary of employees = μ = $5000

Standard deviation = σ = $500

Sample size = n = 40

Required Information:

P(X < $4900) = ?

Answer:

P(X < $4900) = 0.102 = 10.2%

Step-by-step explanation:

We are given a Normal Distribution, which is a continuous probability distribution and is symmetrical around the mean. The shape of this distribution is like a bell curve and most of the data is clustered around the mean. The area under this bell shaped curve represents the probability.

Let X is the random variable that represents the salary of employees at company.

`P(X < \$ 4900) = P(Z < (x - \mu)/((\sigma)/(√(n) ) ) )\\\\P(X < \$4900) = P(Z < (4900 - 5000)/((500)/(√(40) ) ) )\\\\P(X < \$4900) = P(Z < (4900 - 5000)/(79) )\\\\P(X < \$4900) = P(Z < (-100)/(79) )\\\\P(X < \$4900) = P(Z < -1.27)\\`

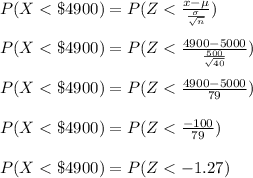
The z-score corresponding to -1.27 from the z-table is 0.102

`P(X < \$4900) = 0.102\\P(X < \$4900) = 10.2 \%`

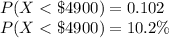
Therefore, there is 10.2% probability that the salary of a randomly selected employee will be less than $4900.

How to use z-table?

Step 1:

In the z-table, find the two-digit number on the left side corresponding to your z-score.(e.g -1.2, 2.2, etc.)

Step 2:

Then look up at the top of z-table to find the remaining decimal point in the range of 0.00 to 0.09. (e.g. if you are looking for 1.27 then go for 0.07 column)

Step 3:

Finally, find the corresponding probability from the z-table at the intersection of step 1 and step 2.