Answer:
F = 6.70N, 26.56° east-north
Step-by-step explanation:
To find the value of the resultant force you first calculate the components x and y of the final force (para encontrar el valor de la fuerza resultante primero hallas los valores de las componentes de la fuerza):
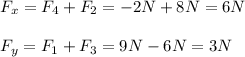
Next, you calculate the magnitude of the force by using the following formula (Luego, calculas la magnitude de F usando la siguiente formula):
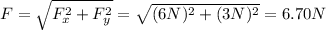
and the direction of the final force is (y la dirección de la fuerza está dada por):
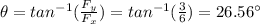
hence, the resultant force has a magnitude of 6.70N and a direction of 26.56° east-north (por lo tanto, la fuerza resultante tiene una magnitud de 6.70N y una dirección de 26.56° este-norte)