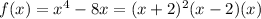Question

Find constants c and d such that f(x)=x4 +cx + d is divisible by (x+2)2.

(That means when f(x) is divided by (x+2)2, remainder is 0)​

Answer 1

d=0, c=-8

Explanation:

We have that
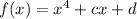`f(x)= x^4+cx+d`. We want f is divisible by
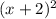`(x+2)^2`. This means that

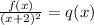`(f(x))/((x+2)^2)=q(x)` or
`f(x) = (x+2)^2q(x)`

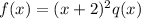
where q is a polynomial of degree less than 4 (since f is a polynomial of degree 4). In this case, since f is of degree 4 and (x+2)^2 is of degree 2, we have that q(x) is of degree 2(this is because when we multiply polynomials they degree adds up).

Then, q(x) is of the form
`(ex^2+fx+g)`.

We can expand the right hand side so

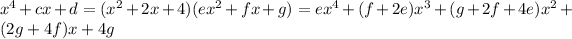`x^4+cx+d = (x^2+2x+4)(ex^2+fx+g)= ex^4+(f+2e)x^3+(g+2f+4e)x^2+(2g+4f)x+4g`. Since both polynomials are equal,the coefficients of each power of x, on both sides, must be equal.Then, we have the equations

`e=1, (f+2e)=0, g+2f+4e=g+2(f+2e)=0, 2g+4f=c, 4g = d`

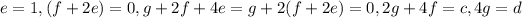
From the first three equations we get that e=1, f=-2, g=0. Then, from the last two equations we get that d=0 and c=-8.

We can check that the polynomial

`f(x) = x^4-8x = (x+2)^2(x-2)(x)`

Answer 2

c=32, d=48

Explanation:

(Ax²+Bx+C)(x+2)²= x⁴+cx+d

Ax⁴+Bx³+Cx²+4Ax³+4Bx²+4Cx+4Ax²+4Bx+4C= x⁴+cx+d

Equating coeeficients on both sides

A=1

B+4A= 0

B=-4

C+4B+4A=0

C=12

4C+4B=c

c=32

4C=d

d=48