Question

Propane at 0.1 MPa, 20o C enters an insulated compressor operating at steady state and exits at 0.4 MPa, 90o C. Neglecting kinetic and potential energy effects, determine a) the power required by the compressor (kJ/kg) b) the change in specific entropy of propane (kJ/kg K) at the outlet and the inlet of the compressor.

Answer 1

a) - 122 kJ/kg

b) 0.117 kJ/kg K

Step-by-step explanation:

Given that:

at inlet condition:

Pressure
`P_1 = 0.1 \ MPa`

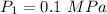
Temperature
`T_1 = 20^0 \ C`

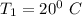
at Outlet condition:

Pressure
`P_2 = 0.4 \ MPa`

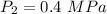
Temperature
`T_2 = 90^ ^0 } \ C`

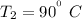
Heat transfer Q = 0

determine a) the power required by the compressor (kJ/kg)

Applying energy equation to the compressor work by the equation:

`W _c = h_1 -h_2`

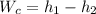
from propane of tables at the given conditions of temperature and pressure; we obtain the following enthalpies

`h_1 = 517.6 \ kJ/kg \\ \\ h_2 = 639.6 \ kJ/kg`

`W_c = 517.6 - 639 .6`

`W_c = - 122 \ \ kJ/kg`

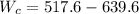
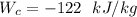
Thus, the power required by the compressor is - 122 kJ/kg

b) the change in specific entropy of propane (kJ/kg K) at the outlet and the inlet of the compressor.

Taking entropies from the propane tables at given conditions of pressure and temperature

`s_1 = 2.194 \ kJ/kgK\\`

`s_2 = 2.311 \ kJ/kgK`

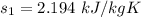
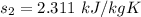
Thus; the rate of entropy production is :

`s_(prod.) = s_2-s_1 \\ \\ s_(prod.) = (2.311 - 2.194 ) kJ/kgK \\ \\`

`s_(prod.) = 0.117 \ kJ/kgK`

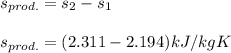
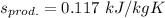
Thus; the change in specific entropy of propane (kJ/kg K) at the outlet and the inlet of the compressor is 0.117 kJ/kg K