Question

Find the center and the radius of the circle with the equation:

x2 + 2x + y2 – 2y - 14 = 0

a. center: (1,-1)

C. center: (2,-2)

radius: 4

radius: 14

b. center: (-1,1)

d. center: (-2,2)

radius: 4

radius: 14

Please select the best answer from the choices provided

Answer 1

B. Center: (-1,1)

radius: 4

Explanation:

Answer 2

`(x+1)^2 + (y-1)^2 = 16`

And the general formula for a circle is given by this expression:

`(x-h)^2 +(y-k)^2 = r^2`

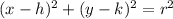
With the center (h,k) and the radius r. If we compare this general expression with the formula that we obtain in (1) we see that :

`h = -1, k =1 , r =4`

So then the best solution for this cae would be:

b. center: (-1,1)

radius =4

Explanation:

For this case we have the following equation given:

`x^2 +2x + y^2 -2y -14=0`

And we can complete the squares for this case like this:

`x^2 +2x +(2/2)^2 +y^2 -2y +(2/2)^2 =14 +1+1`

`(x^2 +2x +1) +(y^2 -2y +1) =16`

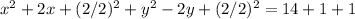
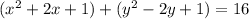
Now we can rewrite the last expression like this:

`(x+1)^2 + (y-1)^2 = 16`

And the general formula for a circle is given by this expression:

`(x-h)^2 +(y-k)^2 = r^2`

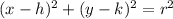
With the center (h,k) and the radius r. If we compare this general expression with the formula that we obtain in (1) we see that :

`h = -1, k =1 , r =4`

So then the best solution for this cae would be:

b. center: (-1,1)

radius =4