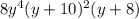Answer:
LCM =
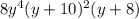
Explanation:
Making factors of
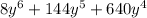
Taking
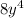 common:
common:
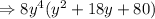
Using factorization method:
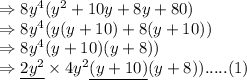
Now, Making factors of
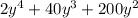
Taking
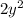 common:
common:
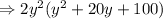
Using factorization method:
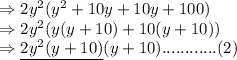
The underlined parts show the Highest Common Factor(HCF).
i.e. HCF is
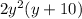 .
.
We know the relation between LCM, HCF of the two numbers 'p' , 'q' and the numbers themselves as:
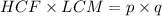
Using equations (1) and (2):
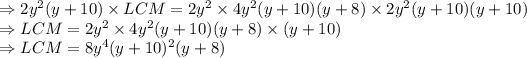
Hence, LCM =