Question

Question 1: The management of a grocery store has kept a record of bad checks received per day for a period of 200 days. The data are shown below. Number of Bad Checks Received Number of Days 0 8 1 12 2 20 3 60 4 40 5 30 6 20 7 10 Develop a probability distribution for the above data. Determine the cumulative probability distribution. What is the probability that in a given day the store receives four or less bad checks? What is the probability that in a given day the store receives more than 3 bad checks?

Answer 1

The probability that in a given day the store receives four or less bad checks is 0.70.

The probability that in a given day the store receives more than 3 bad checks is 0.50.

Explanation:

The data provided shows the number of bad checks received by the management of a grocery store for a period of 200 days.

The probability distribution and the cumulative probability distribution are shown in the table attached below.

Let the number of bad checks received in a day be represented by X.

Compute the probability that in a given day the store receives four or less bad checks as follows:

P (X ≤ 4) = P (X = 0) + P (X = 1) + P (X = 2) + P (X = 3) + P (X = 4)

`=0.04+0.06+0.10+0.30+0.20\\\\=0.70`

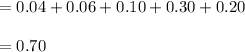
Thus, the probability that in a given day the store receives four or less bad checks is 0.70.

Compute the probability that in a given day the store receives more than 3 bad checks as follows:

P (X > 3) = 1 - P (X ≤ 3)

= 1 - [P (X = 0) + P (X = 1) + P (X = 2) + P (X = 3)]

`=1-[0.04+0.06+0.10+0.30]\\=1-0.50\\=0.50`

Thus, the probability that in a given day the store receives more than 3 bad checks is 0.50.