Question

Find the volume of the right cone. Round your answer to the nearest hundredth.

A right cone with the diameter of the base labeled 14 yards. The angle between the height and slant height measures 32 degrees. The right angle formed the diameter and the height is marked.


The volume is about

cubic yards.

Answer 1

574.82 cubic yards

Explanation:

The diameter of the cone =14 yards

The angle between the height and slant height measures 32 degrees.

First, we determine the height of the cone using trigonometry.

In Right Triangle AOB,

`Tan 32=(7)/(|AO|) \\|AO|*Tan 32 =7\\$Height of the Cone, $|AO|=(7)/(Tan 32) =11.2023 \:yards`

`\text{Volume of a Cone=}(1)/(3)\pi r^2h\\Volume =(1)/(3)\pi*7^2*11.2023\\=574.82$ cubic yards`

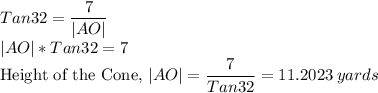
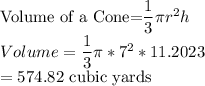
The volume is about 575 cubic yards.