Answer:
It is neither linear nor exponential.
Explanation:
x values: −10,−3, 4, 11
y values: 1, 6, 30, 120
Slope = rate of change
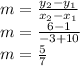
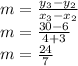
Since rate of change is not constant . So, It is not linear
If the average rate of change is constant, then the function is linear.
If the ratio of consecutive outputs is constant, then the function is exponential.
So,
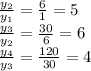
Since the ratio of consecutive outputs is not constant.
So, It is not exponential
Hence it is neither linear nor exponential.