Question

What is the solution of the system of equation? y=2x-3 , 4x-3y=31

Answer 1

Use Substitution.

Plug in 2x-3 in place of y in the second equation.

4x - 3(2x-3) = 31

4x - 6x + 9 =31

-9 -9

-----------------------

-2x=22 so x=-11

Then, y=2(-11)-3, so y=-25

So the solution would be (-11,-25).

Explanation:

is the variable alone?

No

what is it attached to?

you always do adding or subtracting first so it is attached to 3

How is it attached?

by subtraction

what is the inverse operation?

it is addition

then all you do is the same thing but with multiplication or division

Answer 2

Hi!

We can solve this using the substitution method.

Given:

`y=2x-3\\4x-3y=31`

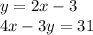
Using the first question, we know that
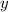`y` is equal to
`2x-3`, so we can simply plug that value in to the second equation, like so:

`4x-3(2x-3)=31`

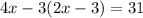
Now, we can algebraically solve this for
`y`

`4x-3(2x-3)=31`

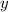
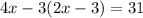
Distribute.

`4x-6x+9=31`

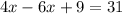
Add like terms.

`-2x+9=31`

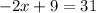
Subtract
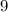`9` from both sides.

`-2x=22`

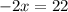
Divide both sides by
`-2`

`x=-11`

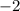
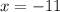
Now plug in that value to the first equation:

`y=2(-11)-3`

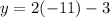
Multiply.

`y=-22-3`

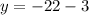
Subtract.

`y=-25`

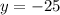
The solution is (-11, -25)