Question

A sphere is inscribed in a cube with a volume of 27 cubic inches. What is the volume of the sphere? Round your answer to the nearest whole number.

The volume of the sphere is approximately

_____ cubic inches.

Answer 1

About 14 cubic inches

Explanation:

We know that a cube has all equivalent side lengths so that the side lengths cubed equals the volume.

`\sqrt[3]{27}` = 3

Now, why do we need this? Well, if the sphere is inscribed in the cube, that means it's touching the side (think back to 2d polygons inscribed in each other). So, each side length of the cube would be the diameter of our sphere.

Because we need the radius to find the sphere's volume, 3/2 = 1.5 (the diameter is twice the radius).

The formula for the volume of a sphere is 4/3(
`r^(3)` x
`\pi`)

When we plug in our values- 4/3(3.375
`\pi`)

Once you solve and round to the nearest whole number, the answer is 14.

Answer 2

51.47 cubic inches

Explanation:

Given the volume of the sphere is: 27 cubic inches

As the know, the following formula used to determine the volume of a sphere:

V = 4/3 πr³ where r is the radius of the sphere

In this situation, we have: V = 27 cubic inches

<=> 4/3 πr³ = 27

<=> r³ = 81/4π

<=> r = 1.86

However, the length of side of the cube is 2 times the radius of the sphere when the sphere is inside the cube

=> the length of the side = 2r = 2*1.86 = 3.72 inches

=> the volume of the cube is:
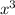`x^(3)` where x is the length of the side

<=> V =
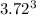`3.72^(3)` = 51.47 cubic inches

Hope it will find you well