Question

A 100-ft3/s water jet is moving in the positive x-direction at 18 ft/s. The stream hits a stationary splitter such that half of the flow is diverted upward at 45° and the other half is directed downward, and both streams have a final speed of 18 ft/s. Disregarding gravitational effects, determine the x- and z-components of the force required to hold the splitter in place against the water force.

Answer 1

Step-by-step explanation:

To start with the mass at the entrance of the channel

`m = \rho V`

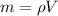
where

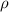`\rho` = density of water = 62.37 lb/ft³

V = velocity of the flow = 100 ft³/s

m = 62.37 lb/ft³ × 100 ft³/s

m = 6237 lb/s

m = 62.37 × 10² lb/s

Since the channels are identical, the mass flow rate are as well equal in both sections i.e

`m_1 = m_2`

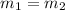
Also; the flow rate is noted to be at a steady state, frictionless and the fluid is deemed to be incompressible

Therefore using the law of conservation of mass flow:

m =
`m_1 +m_2`

m =
`2m_1`

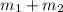
`m_1 = (1)/(2)m`

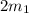
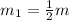
Applying the momentum equilibrium for steady one-dimensional flow:

`\sum F ^ {\to} = \sum_(out) \beta m V^ {\to} - \sum_(in) \beta m V^ {\to}`

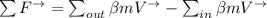
Considering the momentum equation along the x-axis is:

`F_(Rx) = m_1V_1cos \theta _1 + m_2V_2 cos \theta_2 -mV`

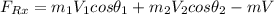
where;

m = mass flow rate before hitting the splliter

V = velocity of flow before hitting the splliter

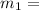`m_1 =`mass flow rate channel one

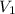`V_1` = velocity flow rate channel one

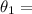`\theta _1 =` angle by the spit channel one to the horizontal

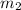`m_2` = mass flow rate channel two

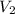`V_2` = velocity flow rate channel two

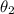`\theta _2` = angle by the spit channel two to the horizontal

From the above recent equation:

`F_(Rx) = (m)/(2) V_1cos \theta _1 + (m)/(2)V_2 cos \theta_2 -mV`

`F_(Rx) = (1)/(2) m V(cos \theta _1 +cos \theta_2) -mV`

`F_(Rx) = m V((cos \theta _1 +cos \theta_2)/(2) -1)`

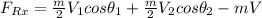
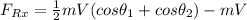
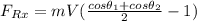
Replacing our values :

`F_(Rx) = 62.37*10^2*18((cos 45^0 +cos 315^0)/(2) -1)`

`F_(Rx) = 62.37*10^2*18({0.707-1)`

`F_(Rx) = -32,893.938 \ lb`

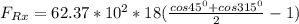
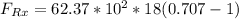
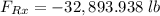
Thus, the force needed in the x-direction to keep the splliter position is 32,893.938 lb (i.e in the opposite direction of the water jet)

Again:

`\sum F ^ {\to} = \sum_(out) \beta m V^ {\to} - \sum_(in) \beta m V^ {\to}`

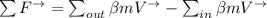
Considering the momentum equation along the z-axis is:

`F_(Rx) = m_1V_1sin \theta _1 + m_2V_2 sin \theta_2 -0`

`F_(Rx) = (m)/(2) V_1sin \theta _1 + (m)/(2)V_2 sin \theta_2`

`F_(Rx) = (m)/(2) V_1(sin \theta _1 +sin \theta_2})`

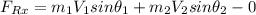
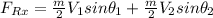
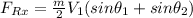
Replacing our values :

`F_(Rx) = (62.37*10^2)/(2) *18(sin 45^0 +sin 315^0})`

`F_(Rx) = 0`

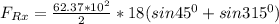
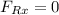
Thus, there is no force needed in the z-direction. Since the forces are equal and opposite in direction to each other.