Answer:
The smallest sample size required to obtain the desired margin of error is 44.
Explanation:
I think there was a small typing error, we have that
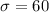 is the standard deviation of these weighs.
is the standard deviation of these weighs.
We have that to find our
 level, that is the subtraction of 1 by the confidence interval divided by 2. So:
level, that is the subtraction of 1 by the confidence interval divided by 2. So:
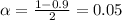
Now, we have to find z in the Ztable as such z has a pvalue of
 .
.
So it is z with a pvalue of
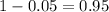 , so
, so
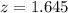
Now, find the margin of error M as such
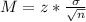
Which of these is the smallest approximate sample size required to obtain the desired margin of error?
This sample size is n.
n is found when
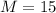
So
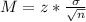

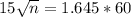
Simplifying by 15
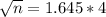


Rounding up
The smallest sample size required to obtain the desired margin of error is 44.