Question

Gerry plans to place a 24 -foot ladder against the side of his house. The bottom of the ladder will be 8 feet from the house. How far up the side of the house will the ladder reach? Answer exactly or round to 2 decimal places.

Answer 1

x = 22,63 ft

Explanation:

The side of the house, the ladder and the ground form a right triangle. The hypotenuse is the ladder ( 24 ft) and the legs are the side of the house (x uknown ) and the other leg, is distance between bottom of the ladder and the side of the house, therefore

Pytagoras Theorem :

H² = L₁² + L₂²

(24)² = (8)² + x²

x² = (24)² - (8)²

x² = 576 - 64 ⇒ x² = 512

x = 22,63 ft

Answer 2

22.63 ft

Explanation:

In the right triangle ABC attached,

AB is the length of the ladder which is the hypotenuse

AC is the distance of the ladder's bottom from the house.

We are to determine how far up the side of the house the ladder will reach.

We apply Pythagoras Theorem to solve this.

`\overline{AB}^2=\overline{AC}^2+\overline{BC}^2\\24^2=8^2+\overline{BC}^2\\\overline{BC}^2=576-64\\\overline{BC}^2=512\\BC=√(512)=22.63 ft`

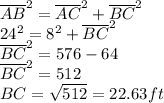
The ladder will reach 22.63 ft (correct to 2 decimal places) up the wall of the house.