Question

A ball is being inflated at a rate that can be modeled by the function V(t) = 10t, where t is the number of seconds spent inflating the ball. The radius at a given volume can be modeled by the function

Answer 1

`r = \sqrt[3]{7.5 t/\pi} \\`

Explanation:

Given volume as a function of time is for a ball is V(t) = 10t

we know that volume of a sphere is given by
`(4/3) *\pi * r^3`

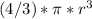
where r is radius of sphere

Note we are using formula for sphere as ball is spherical in shape

Now equating volume V(t) = 10t, and volume of a sphere is given by formula
`(4/3) *\pi * r^3`

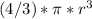
`10t = (4/3 ) \pi r^3\\=> 10t * 3/4 = \pi r^3\\=>(10t * (3/4))/\pi = r^3\\=> r^3= (30/4)*t /\pi = 7.5 t/\pi \\=> r = \sqrt[3]{7.5 t/\pi} \\\\or \\ r = ({7.5 t/\pi})^1/3`

Hence radius at a given volume can be modeled by function

`=> r = \sqrt[3]{7.5 t/\pi} \\\\\\`