Question

A boss wants to show that productivity decreases when the boss leaves the office. A office of 26 employees handed in productivity reports when the boss was absent (M1-5, SS1-250) compared to 36 employees who handed in reports when the boss was present (M2-8, SS2-420)

a) What is the null and alternative hypothesis?

b) Compute t ?

c) Compute df?

d) Given the a-0.05, compute the negative value obt oft ?

e) Ist significant, Yes or No?

Answer 1

a) The null and alternative hypotesis are:

`H_0: \mu_1-\mu_2=0\\\\H_a: \mu_1-\mu_2<0`

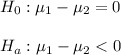
1: productivity when boss absent, 2: productivity when boss present

b) t=-3.492

c) df=60

d) tc=-1.6706

e) Yes, it is significant.

Explanation:

Hypothesis test for the difference between means.

The claim is that productivity decreases when the boss leaves the office.

Then, the null and alternative hypotesis are:

`H_0: \mu_1-\mu_2=0\\\\H_a: \mu_1-\mu_2<0`

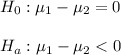
The significance level is α=0.05.

The degrees of freedom are calculated as:

`df=(n_1-1)+(n_2-1)=(26-1)+(36-1)=60`

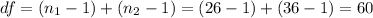
The difference between sample means Md is:

`M_d=M_1-M_2=5-8=-3`

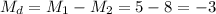
Now, we have to calculate the standard error for the difference of the means.

As the sample sizes are not equal, we have to calculate the harmonic mean of the sample size:

`n=(2)/(1/n_1+1/n_2)=(2)/(1/26+1/36)=(2)/(0.066)=30.194`

The standard deviation of sample 1 (boss absent) is:

`s_1=\sqrt{(SS_1)/(n_1-1)}=\sqrt{(250)/(26-1)}=√(10)=3.16`

The standard deviation of sample 2 (boss present) is:

`s_2=\sqrt{(SS_2)/(n_2-1)}=\sqrt{(420)/(36-1)}=√(12)=3.46`

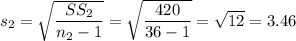
We calculate the mean square error (MSE) as:

`MSE=((n_1-1)s_1^2+(n_2-1)s_2^2)/((n_1-1)+(n_2-1))=(25\cdot 3.16^2+35\cdot 3.46^2)/(60)=(249.64+419.006)/(60)\\\\\\MSE=(668.646)/(60)\\\\\\MSE=11.14`

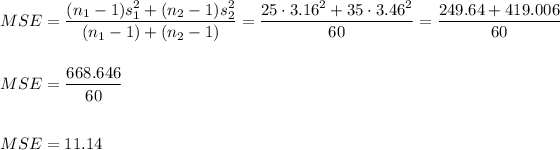
Then, the standard error can be calculated as:

`s_(M_d)=\sqrt{(2MSE)/(n)}=\sqrt{(2\cdot 11.14)/(30.194)}=0.86`

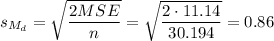
Now, we can calculate the test statistic t:

`t=(M_d-(\mu_1-\mu_2))/(s_(M_d))=(-3-(0))/(0.86)=-3.492`

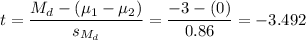
If we apply the critical value approach, the critical value of t for a significance level α=0.05 and 60 degrees of freedom is:

`t_c=-1.6706`

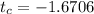
As this is a left-tail test, the decision rule is to reject the null hypothesis if the test statistic is smaller than the critical value.

In this case, the test statistic t=-3.492 is smaller than the critical value t_c=-1.6706, the effect is significant.