Question

Veterinarians use different medications to treat dogs for fleas. Once administered, the medication typically decays exponentially. One treatment decays by half each week.

A dog receives 4 mL of medication and the function f gives the number of mL of medicine left after w weeks.


f(x) = 4 (1/2)^w


Reply as ansers 1a, 1b, 1c, 2.


Find the amount of medication in the dog’s bloodstream 1 week, 2 weeks, and 3 weeks after it is administered.


a.) 1 week b.) 2 weeks c) 3 weeks.


Explain what F(4/7)

means in this context. The 7 means the number of days in 1 week.

Answer 1

(a) The amount of medication in the dog’s bloodstream 1 week is 2 ml.

(b) The amount of medication in the dog’s bloodstream 2 weeks is 1 ml.

(c) The amount of medication in the dog’s bloodstream 3 weeks is 0.50 ml.

Explanation:

The decay function is:

`y=a(1-r)^(t)`

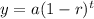
Here,

y = final amount

a = initial amount

r = decay rate

t = time

The function representing the number of ml of medicine left after w weeks, when a dog receives 4 ml of medication is:

`f(x)=4\cdot ((1)/(2))^(w)`

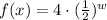
(a)

Compute the amount of medication in the dog’s bloodstream 1 week as follows:

`f(x)=4\cdot ((1)/(2))^(w)\\\\f(1)=4\cdot ((1)/(2))^(1)\\\\=4*(1)/(2)\\\\=2\ \text{ml}`

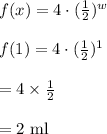
Thus, the amount of medication in the dog’s bloodstream 1 week is 2 ml.

(b)

Compute the amount of medication in the dog’s bloodstream 2 weeks as follows:

`f(x)=4\cdot ((1)/(2))^(w)\\\\f(2)=4\cdot ((1)/(2))^(2)\\\\=4*(1)/(4)\\\\=1\ \text{ml}`

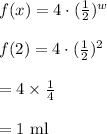
Thus, the amount of medication in the dog’s bloodstream 2 weeks is 1 ml.

(c)

Compute the amount of medication in the dog’s bloodstream 3 weeks as follows:

`f(x)=4\cdot ((1)/(2))^(w)\\\\f(3)=4\cdot ((1)/(2))^(3)\\\\=4*(1)/(8)\\\\=0.50\ \text{ml}`

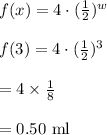
Thus, the amount of medication in the dog’s bloodstream 3 weeks is 0.50 ml.