Question

A certain radioactive isotope decays at a rate of 0.125% per year. Determine the half-life of this isotope, to the nearest year.

Answer 1

The half-life of this isotope is of 554 years.

Explanation:

The amount of the radioactive isotope remaining after t years is given by the following equation:

`P(t) = P(0)(1-r)^(t)`

In which P(0) is the initial amount and r is the yearly rate that it decays, as a decimal.

A certain radioactive isotope decays at a rate of 0.125% per year.

This means that
`r = 0.00125`

Then

`P(t) = P(0)(1-0.00125)^(t)`

`P(t) = P(0)(0.99875)^(t)`

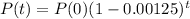
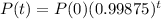
Determine the half-life of this isotope, to the nearest year.

This t for which
`P(t) = 0.5P(0)`

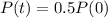
Then

`P(t) = P(0)(0.99875)^(t)`

`0.5P(0) = P(0)(0.99875)^(t)`

`(0.99875)^(t) = 0.5`

`\log{(0.99875)^(t)} = \log{0.5}`

`t\log{0.99875} = \log{0.5}`

`t = \frac{\log{0.5}}{\log{0.99875}}`

`t = 554.17`

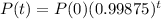
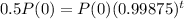
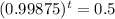
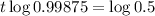
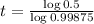
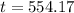
Rounding to the neearest year

The half-life of this isotope is of 554 years.