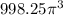Answer:
the area of the sector with a central angle of 11/6π radians is equal to
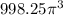
Explanation:
The area A of the entire circle is given by:
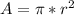
Where r is the radius of the circle. So the area of a circle with radius
 is:
is:
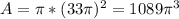
Additionally an entire circle has a central angle of
 radians.
radians.
So, we can calculate the area of a sector using the rule of three in which we know that
 radians has an Area of
radians has an Area of
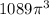 then what is the area of the sector with a central angle of 11/6π radians as:
then what is the area of the sector with a central angle of 11/6π radians as:
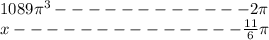
Where x is the area of the sector with a central angle of 11/6π radians.
Finally, solving for x, we get:
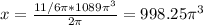
So, the area of the sector with a central angle of 11/6π radians is equal to