Answer:
Explanation:
Let the side of the square base be a cm and height be h cm.
volume = a²h = 256000
area of base + lid = 2a²
area of side wall = 4ah
Total cost C = 10 x 2a² + 2.5 x 4ah
C = 20 a² + 10 ah
= 20 a² + 10 a x
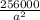
= 20 a² +
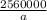
differentiating

for minimum cost

a³ = 64000
a = 40 cm
length of side base = 40 cm
height h =
40 x 40 x h = 256000
h = 160 cm
cost = 20 a² + 10 ah
= 20 x 40² + 10 x 40 x 160
= 32000+64000
= 96000 .