Question

A different rectangle has a diagonal of 60 yards and a height of 40 yards. Find the width of the rectangle rounded to the nearest hundredth.

Answer 1

`60^2 -40^2 = x^2`

`3600 -1600 =x^2`

`2000 = x^2`

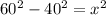
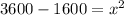
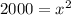
And taking square root in both sides we got:

`x  =√(2000 yd^2) = 44.72 yd`

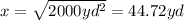
So then the width for this case is 44.72 yd

Explanation:

We create a figure with the conditions given and we can see it on the figure attached with 60 yd the diagonal and 40 yd the height and x the width.

From the lower right triangle if we use the theorem of Pythagoras, we assume the the hypothenuse is 60 yd and the opposite side is 40 yd then we have:

`60^2 = 40^2 + x^2`

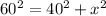
And x represent for this case the width of the rectangle. If we solve for x^2 we can subtract
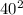`40^2` from both sides and we got:

`60^2 -40^2 = x^2`

`3600 -1600 =x^2`

`2000 = x^2`

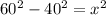
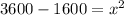
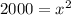
And taking square root in both sides we got:

`x  =√(2000 yd^2) = 44.72 yd`

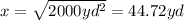
So then the width for this case is 44.72 yd