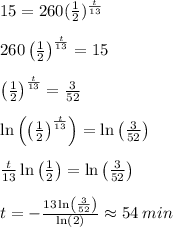Answer:
It would take 54 minutes to the element X to decay to 15 grams.
Explanation:
A radioactive half-life refers to the amount of time it takes for half of the original isotope to decay and its given by
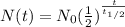
where,
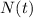 = quantity of the substance remaining
= quantity of the substance remaining
 = initial quantity of the substance
= initial quantity of the substance
 = time elapsed
= time elapsed
 = half life of the substance
= half life of the substance
We know that the element X decays radioactively with a half life of 13 minutes (
 ), there are 260 grams of it (
), there are 260 grams of it (
 ) and we want to find how long (
) and we want to find how long (
 ) would it take the element to decay to 15 grams (
) would it take the element to decay to 15 grams (
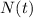 ).
).
Using the above formula and solving for
 , we get that
, we get that