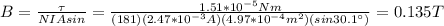Answer:
B = 0.135T
Step-by-step explanation:
To find the magnitude of the magnetic field you use the following formula, for the torque produced by a magnetic field B in a loop:
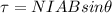 (1)
(1)
τ: torque = 1.51*10^-5 Nm
I: current = 2.47mA = 2.47*10^-3 A
B: magnitude of the magnetic field
A: area of the loop = 4.97cm^2 = 4.97(10^-2m)^2=4.97*10^-4m^2
N: turns = 181
θ: angle between B and the magnetic dipole (same as the direction of the normal to the plane)
You replace the values of the parameters in (1). Furthermore you do B the subject of the formula: