Question

Simplify the expression cos x cot x+ sin x please select the best answer from the choices provided a.0, b.csc x, c. Tan x, d sec x

Answer 1

`cot x = (cos x)/(sin x)`

`cos x (cos x)/(sin x) + sin x`

`(cos^2 x)/(sin x) +sin x`

`sin^2 x + cos^2 x =1`

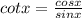
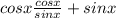
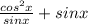
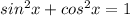
Solving for
`cos^2 x` we got
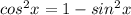`cos^2 x =1 -sin^2 x` and replacing this we got:

`(1-sin^2 x)/(sin x) +sin x`

`(1)/(sin x) -(sin^2 x)/(sin x) +sin x`

`csc x -sin x + sin x = csc x`

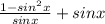
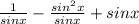
And then the best option for this case would be:

b.csc x

Explanation:

For this case we have the following expression given:

`cos x cot x + sin x`

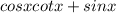
We know from math properties that the definition for cot is
`cot x = (cos x)/(sin x)`

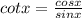
If we use this definition we got:

`cos x (cos x)/(sin x) + sin x`

`(cos^2 x)/(sin x) +sin x`

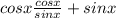
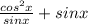
Now we can use the following identity:

`sin^2 x + cos^2 x =1`

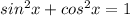
Solving for
`cos^2 x` we got
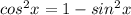`cos^2 x =1 -sin^2 x` and replacing this we got:

`(1-sin^2 x)/(sin x) +sin x`

`(1)/(sin x) -(sin^2 x)/(sin x) +sin x`

`csc x -sin x + sin x = csc x`

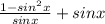
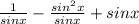
And then the best option for this case would be:

b.csc x