Question

A food company sells salmon to various customers. The mean weight of the salmon is 25 lb with a standard deviation of 4 lbs. The company ships them to restaurants in boxes of 4 ​salmon, to grocery stores in cartons of 16 ​salmon, and to discount outlet stores in pallets of 121 salmon. To forecast​ costs, the shipping department needs to estimate the standard deviation of the mean weight of the salmon in each type of shipment. Complete parts​ (a) and​ (b) below. ​a) Find the standard deviations of the mean weight of the salmon in each type of shipment. Find the standard deviation of the mean weight of the salmon in the boxes sold to restaurants.

Answer 1

The standard deviation of the mean weight of the salmon in the boxes sold to restaurants is of 2 lbs.

The standard deviation of the mean weight of the salmon in cartons sold to grocery stores is of 1 lb.

The standard deviation of the mean weight of the salmon in in pallets sold to discount outlet stores is of 0.3636lb.

Explanation:

The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean
`\mu` and standard deviation
`\sigma`, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
`\mu` and standard deviation
`s = (\sigma)/(√(n))`.

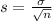In this question, we have that:

`\sigma = 4`

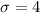
To restaurants:

Boxes of 4 salmon, so
`n = 4`

Then

`s = (\sigma)/(√(n)) = (4)/(√(4)) = 2`

The standard deviation of the mean weight of the salmon in the boxes sold to restaurants is of 2 lbs.

To grocery stores:

Cartons of 16 ​salmon, so
`n = 16`

Then

`s = (\sigma)/(√(n)) = (4)/(√(16)) = 1`

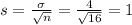
The standard deviation of the mean weight of the salmon in cartons sold to grocery stores is of 1 lb.

To discount outlet stores:

Pallets of 121 salmon.

Then

`s = (\sigma)/(√(n)) = (4)/(√(121)) = 0.3636`

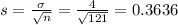
The standard deviation of the mean weight of the salmon in in pallets sold to discount outlet stores is of 0.3636lb.