Question

The bore diameters of eight randomly selected bearings are shown here (in mm): 50.001, 50.002, 49.998, 50.006, 50.005, 49.996, 50.003, 50.004 a) Calculate the sample average. B) Calculate the sample standard deviation.

Answer 1

sample average = 50.00187

sample standard deviation = 0.0034

Step-by-step explanation:

given data

8 diameters = 50.001, 50.002, 49.998, 50.006, 50.005, 49.996, 50.003, 50.004

solution

first we get her sample average that is express as

sample average =
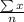`(\sum x)/(n)` ...............1

here x is diameter of bearing

and n is total no of sample

put here value and we get

sample average =
`(400.015)/(8)`

sample average = 50.00187

and

now we get here sample standard deviation

sample standard deviation =
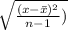`\sqrt{((x-\bar x )^2)/(n- 1))` ...............2

put here value and we get

sample standard deviation =
`\sqrt{(00008288)/(8- 1))`

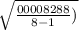
sample standard deviation = 0.0034