Answer:
10 years until the value of the car is 11000 dollars
Explanation:
The value of the car after t years is modeled by the following equation:

In which V(0) is the initial value and r is the yearly depreciation ratio, as a decimal.
A new car is purchased for 21100 dollars.
This means that
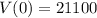
The value of the car depreciates at 6% per year.
This means that
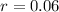 . So
. So

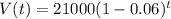
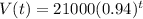
To the nearest year, how long will it be until the value of the car is 11000 dollars?
This is t when
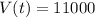
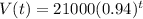
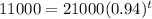
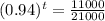

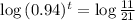
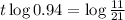
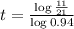
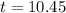
To the nearest year
10 years until the value of the car is 11000 dollars