Answer:
The probability that all 3 suppliers will be disrupted at the same time at some point during the next five years is 0.0023.
Explanation:
The formula to compute the probability that n suppliers will be disrupted at the same time for a supply cycle is:
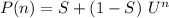
Here,
S = super event
U = unique event
n = number of suppliers.
The information provided is:
S = 0.23% = 0.0023
U = 1.4% = 0.014
n = 3
Compute the probability that all 3 suppliers will be disrupted at the same time at some point during the next five years as follows:
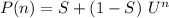
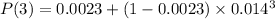
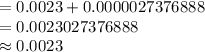
Thus, the probability that all 3 suppliers will be disrupted at the same time at some point during the next five years is 0.0023.