Question

A poll finds that 54% of the 600 people polled favor the incumbent. Shortly after the poll is taken, it is disclosed that the incumbent had an extramarital affair. A new poll finds that 50% of the 1030 polled now favor the incumbent. We want to know if his support has decreased. The test statistic is

Answer 1

The value of z test statistics is 1.561.

Explanation:

We are given that a poll finds that 54% of the 600 people polled favor the incumbent.

Shortly after the poll is taken, it is disclosed that the incumbent had an extramarital affair. A new poll finds that 50% of the 1030 polled now favor the incumbent.

Let
`p_1` = population proportion of people who favor the incumbent in the first poll

`p_2` = population proportion of people who favor the incumbent in the second poll

So, Null Hypothesis,
`H_0` :
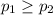`p_1\geq p_2` {means that his support has increased or remained same after the second poll}

Alternate Hypothesis,
`H_0` :
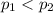`p_1 < p_2` {means that his support has decreased after the second poll}

The test statistics that would be used here is Two-sample z test for proportions;

T.S. =
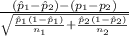`\frac{(\hat p_1-\hat p_2)-(p_1-p_2)}{\sqrt{(\hat p_1(1-\hat p_1))/(n_1)+(\hat p_2(1-\hat p_2))/(n_2) } }` ~ N(0,1)

where,
`\hat p_1` = sample proportion of people who favor the incumbent in first poll = 54%

`\hat p_1` = sample proportion of people who favor the incumbent in second poll = 50%

`n_1` = sample of people in first poll = 600

`n_2` = sample of people in second poll = 1030

So, the test statistics =
`\frac{(0.54-0.50)-(0)}{\sqrt{(0.54(1-0.54))/(600)+(0.50(1-0.50))/(1030) } }`

= 1.561

Hence, the value of z test statistics is 1.561.