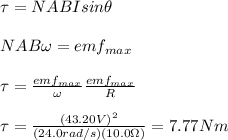Answer:
a) 43.20V
b) 2.71W/s
c) 40.25s
d) 7.77Nm
Step-by-step explanation:
(a) The emf of a rotating coil with N turns is given by:

N: turns
B: magnitude of the magnetic field
A: area
w: angular velocity
the emf max is given by:
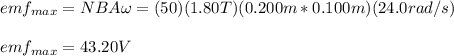
(b) the maximum rate of change of the magnetic flux is given by:
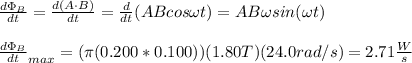
(c)
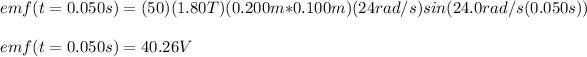
(d) The torque is given by: