Answer:
There are 5,040 distinguishable permutations of 7 letters with the letters of the name PHANTOM.
Explanation:
The letters of the name PHANTOM don't repeat themselves, there is only one of each type fot the 7 letters.
We consider the permutations of 7 letters.
Then, we can calculate the permutations as:
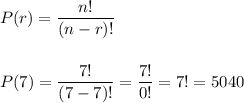
There are 5,040 distinguishable permutations of 7 letters with the letters of the name PHANTOM.