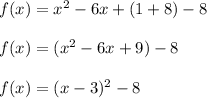Question

How many more unit tiles must be added to the function

f(x)=x2-6x+1 in order to complete the square?

T

Oo oo

BETEREN

ER

00

WEEEEEE

SEPTEMBER

Answer 1

It is necessary to sum 8 units

Explanation:

you have the following polynomial:

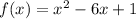`f(x)=x^2-6x+1` (1)

To complete the square you take into account the following general notable product:

`(a-b)^2=a^2-2ab+b^2`

Next, you take into account the coefficient of the second term in (1)

-6x = -2ab

a = x

-6a = -2ab

b = 6/2 = 3

Then, the third term must be:

b^2 = 3^2 = 9

But you have +1. Hence, you must sum 8, and also rest 8 in (1):

`f(x)=x^2-6x+(1+8)-8\\\\f(x)=(x^2-6x+9)-8\\\\f(x)=(x-3)^2-8`