Question

A repair shop believes that people travel more than 3500 miles between oil changes. A random sample of 8 cars getting an oil change has a mean distance of 3375 miles since having an oil change with a standard deviation of 225 miles. At a = 0.05, do you have enough evidence to support the shop’s claim?

Answer 1

There is not enough evidence to support the shop’s claim.

Explanation:

In this case we need to test whether the claim that people travel more than 3500 miles between oil changes is correct or not.

The hypothesis for the test can be defined as follows:

H₀: People travel not more than 3500 miles between oil changes, i.e. μ ≤ 3500.

Hₐ: People travel more than 3500 miles between oil changes, i.e. μ > 3500.

The information provided is:

`n=8\\\bar x=3375\ \text{miles}\\s=225\ \text{miles}\\\alpha =0.05`

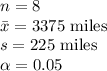
As the population standard deviation is not known we will use a t-test for single mean.

Compute the test statistic value as follows:

`t=(\bar x-\mu)/(s/√(n))=(3375-3500)/(225/√(8))=-1.57`

Thus, the test statistic value is -1.57.

The degrees of freedom of the test is:

df = (n - 1) = 8 - 1 = 7

Compute the p-value of the test as follows:

`p-value=P(t_((n-1))>-1.57)\\=P(t_(7)>-1.57)\\=0.0802`

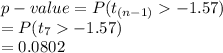
*Use a t-table.

Thus, the p-value of the test is 0.0802.

Decision rule:

If the p-value of the test is less than the significance level then the null hypothesis will be rejected and vice-versa.

p-value = 0.0802 > α = 0.01

The null hypothesis will not be rejected at 5% level of significance.

Thus, concluding that there is not enough evidence to support the shop’s claim that people travel more than 3500 miles between oil changes.