Question

The 11th term in a geometric sequence is 48 and the common ratio is −0.8. The 12th term is _________ and the 10th term is ________.

Answer 1

The 12th term is -38.4 and the 10th term is -60.

Explanation:

Consider the geometric sequence,

`S=\{a,\ ar,\ ar^(2),\ ar^(3),\ ...\}`

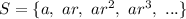
The first term is, a.

The common ratio is, r.

The formula to compute the common ratio is:

`r=(T_(n))/(T_(n-1))`

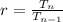
The information provided is:

T₁₁ = 48

r = -0.8

Compute the 12th term as follows:

`r=(T_(n))/(T_(n-1))`

`-0.8=(T_(12))/(T_(11))\\\\0.8=(T_(12))/(48)\\\\T_(12)=48*-0.8\\\\T_(12)=-38.4`

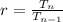
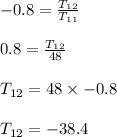
The 12th term of the geometric sequence is -38.4.

Compute the 10th term as follows:

`r=(T_(n))/(T_(n-1))`

`-0.8=(T_(11))/(T_(10))\\\\0.8=(48)/(T_(10))\\\\T_(10)=(48)/(-0.8)\\\\T_(10)=-60`

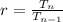
The 10th term of the geometric sequence is -60.