Answer:
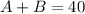 (1)
(1)
 (2)
(2)
From equation (1) we can solve for A and we got:
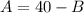 (3)
(3)
And replacing equation (3) into equation (2) we got:
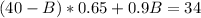
And solving the last equation for B we got:
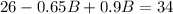
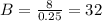
And solving for A from equation (3) we got:

So then we need 8 ounces of solution A with concentration of 65% of salt and 32 ounces of solution B with 90% of salt
Explanation:
Let A represent the amount of solution A and B the amount of solution B. We know that the concentration of A is 65% and the concentration for B is 90%.
We want to obtain a solution of 40 ounces with a concentration of 85% of salt.
Based on this we can set up the following equations:
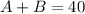 (1)
(1)
 (2)
(2)
From equation (1) we can solve for A and we got:
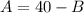 (3)
(3)
And replacing equation (3) into equation (2) we got:
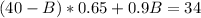
And solving the last equation for B we got:
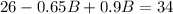
We subtract in both sides 36:
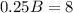
And dividing both sides by 0.25 we got:
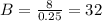
And solving for A from equation (3) we got:

So then we need 8 ounces of solution A with concentration of 65% of salt and 32 ounces of solution B with 90% of salt